引言¶
究竟什么是机器学习?¶
A branch of artificial intelligence, concerns the construction and study of systems that can learn from data. (REF)机器学习算法是一类从数据中自动分析获得规律,并利用规律对未知数据进行预测的算法。
概率 vs. 统计¶
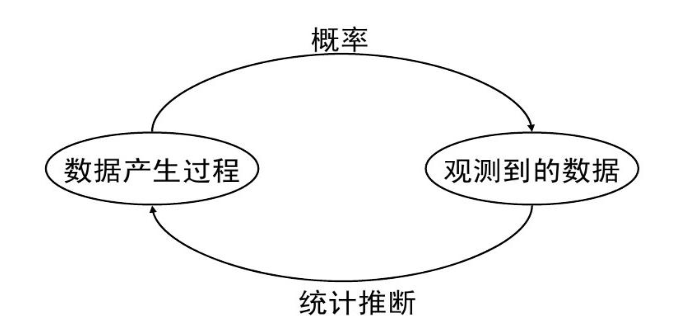
概率:研究随机事件出现的可能性的数学分支,描述非确定性(Uncertainty)的正式语言,是统计推断的基础
- 概率:一个事件或事件集合出现的可能性
- 基本问题:给定以一个数据产生过程,则输出的性质是什么。
统计推断:处理数据分析和概率理论的数学分支,与数据挖掘和机器学习是近亲
- 统计量:一个用以描述样本或总体性质的数值,如均值或方差
- 基本问题:给定输出数据,我们可以得到该数据的产生过程的哪些信息(相当于是“概率”的一个逆过程)
概率统计基础的重要性¶
研究数据分析必须大好概率和统计基础
- Using fancy tools like neural nets, boosting and support vector machines without understanding basic statistics like doing brain surgery before knowing how to use a band-aid.
- 做脑外科手术,却不知道怎么使用绷带!
参考书推荐¶
- Kevin P. Murphy, Machine Learning: A Probabilistic Perspective, MIT Press, 2012
- 统计部分涵盖Larry了的内容,本笔记所用的符号体系来自此书。
- Larry Wasserman, All of Statistics: A Concise Course in Statistical Inference
- 中译本:《统计学完全教程》
- 内容很全,但有些部分篇幅略少,更偏向于从统计的角度讲述,为计算机系所写
- 盛聚/谢式千/潘承毅,概率论与数理统计,高等教育出版社
- 浙大的这本很不错,国产书算是不错的。
概率¶
一、概率公理及推论(基石)¶
概率¶
- 频率学派:多次重复试验(多次抛掷硬币),则我们期望正面向上的次数占总实验次数的一半。
- Bayesian 学派:我们相信下一次试验中,硬币正面向上的可能性为0.5.
- 概率是我们对事情不确定性的定量描述,与信息有关,而非重复实验。
- 可以用来对不能重复实验的时间的不确定,如明天天晴的概率为0.8,如某邮件是垃圾邮件的概率。
样本空间和事件¶
- 将某个事先不知道输出的试验的所有可能结果组成的集合称为该试验的 样本空间。
- 某试验的样本空间的子集为试验的 随机事件。
概率公理¶
- 对某随机试验的每个事件 A,赋予一个实数 \(\mathbb{P}(A)\),称为 A 的概率,如果集合函数 \(P(\cdot)\) 满足下列条件:
- 非负性:对于每一个事件 \(A\),有 \(\mathbb{P}(A)\ge0\)
- 规范性:对于必然事件 \(S\) (样本空间),有 \(\mathbb{P}(S)=1\)
- 可列可加性:对两两不相交(互斥)事件 \(A_i\),即对于 \(A_iA_j\neq\emptyset,i\neq j,i,j=1,2,\dots\),有
从上述三个公理,可推导出概率的所有的其他性质。
推论:
不可满足命题的概率为0
\[\begin{split}\mathbb{P}(\emptyset)=0 \\ \mathbb{P}(A\cap\bar{A)}=0\end{split}\]对任意两个事件 A 和 B
\[\mathbb{P}(A\cup B)=\mathbb{P}(A)+\mathbb{P}(B)-\mathbb{P}(A\cap B)\]事件 A 的补事件
\[\mathbb{P}(\bar{A})=1-\mathbb{P}(A)\]对任意事件 A
\[0 \geq \mathbb{P}(A) \geq 1\]
联合概率 & 条件概率¶
联合概率 表示两个事件共同发生的概率。A 与 B 的联合概率表示为 \(\mathbb{P}(A,B)\) 或者 \(\mathbb{P}(A\cap B)\)。对任意两个事件 A 和 B,
\[\mathbb{P}(A,B)=\mathbb{P}(A\cap B)=\mathbb{P}(A|B)\mathbb{P}(B)\]条件概率 是指事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为:\(\mathbb{P}(A|B)\),读作“在B条件下A的概率”。当 \(\mathbb{P}(B)>0\) 时,给定 B 时 A 的条件概率为
\[\mathbb{P}(A|B)=\frac{\mathbb{P}(A,B)}{\mathbb{P}(B)}\Rightarrow\mathbb{P}(A,B)=\mathbb{P}(A|B)\mathbb{P}(B)\]所谓 积规则(Product Rule)。有穷多个事件的积事件情况:
设 \(A_1,A_2,…,A_n\) 为任意 n 个事件 \((n\ge2)\) 且 \(\mathbb{P}(A_1,A_2,…,A_n)>0\),则
\[\mathbb{P}(A_1,A_2,\cdots,A_n)=\mathbb{P}(A_1)\mathbb{P}(A_2|A_1)\cdots\mathbb{P}(A_n|A_1A_2\cdots A_{n-1})\]给定任意 B,若 \(\mathbb{P}(B)>0\),则 \(\mathbb{P}(\cdot|B)\) 也是一个概率,即满足概率的三个概率公理。
\[\begin{split}\mathbb{P}(A|B)\geqslant0 \,\,\text{非负性}\\ \mathbb{P}(\Omega|B) = 1\,\,\,\,\text{规范性}\\ \mathbb{P}\Big(\bigcup^\infty_{i=1}A_i|B\Big)=\sum^\infty_{i=1}\mathbb{P}\big(A_i|B\big)\,\,\,\,\text{可列可加性}\end{split}\]
贝叶斯公式¶
设 \(B_1,B_2,…,B_n\) 是一组事件,若
\(i\neq j\in\{1,2,…,n\},B_iB_j=\emptyset\)
\(B_1\cup B_2\cup…\cup B_n=\Omega\)
则称 \(B_1,B_2,…,B_n\) 样本空间 \(\Omega\) 的一个 划分 ,或称为样本空间 \(\Omega\) 的一个 完备事件组 。
全概率公式:令 \(A_1,…,A_K\) 为 A 的一个划分,则对任意事件 B,有
\[\mathbb{P}(B)=\sum_j\mathbb{P}(B|A_j)\mathbb{P}(A_j)\]贝叶斯公式:令 \(A_1,…,A_k\) 为 A 的一个划分且对每个 \(k,k=1,2,…,K\) 。若 \(\mathbb{P}(B)>0\),则对每个 \(\mathbb{P}(A_k)>0\) 有( 由条件概率推导贝叶斯公式 )
\[\mathbb{P}(A_k|B)=\frac{\mathbb{P}(B,A_k)}{\mathbb{P}(B)}=\frac{\mathbb{P}(B|A_k)\mathbb{P}(A_k)}{\sum_j\mathbb{P}(B|A_j)\mathbb{P}(A_j)}\]注:上述公式中,分子分母形式相同,分母为所有划分之和。
注: 先验概率 \(\mathbb{P}(A_k)\) 是事情还没有发生,要求这件事情发生的可能性的大小。它往往作为“由因求果”问题中的“因”出现; 后验概率 \(\mathbb{P}(A_k|B)\) 是事情已经发生,要求这件事情发生的原因是由某个因素引起的可能性的大小。是“执果寻因”问题中的“因”。后验概率的计算要以先验概率为基础。
例:贝叶斯公式应用:
已知Macintosh用户、Windows用户和Linux用户感染病毒的概率(先验概率)分别是0.65、0.82和0.5。用户使用Macintosh、Windows和Linux操作系统的比例分别为0.3、0.5和0.2。问现在发现用户感染了病毒,则该用户为Windows用户的概率(后验概率)是多少?
解:令 B 表示被病毒感染这一随机事件,
\(A_1\) 表示Macintosh用户,则 \(\mathbb{P}(A_1)=0.3,\mathbb{P}(B|A_1)=0.65\)
\(A_2\) 表示Windows用户,则 \(\mathbb{P}(A_2)=0.5, \mathbb{P}(B|A_2)=0.82\)
\(A_3\) 表示Linux用户,则 \(\mathbb{P}(A_3)=0.2,\mathbb{P}(B|A_3)=0.5\)
因为 \(\mathbb{P}(A_1)+\mathbb{P}(A_2)+\mathbb{P}(A_3)=1\) ,所以 \(A_1、A_2\) 和 \(A_3\) 组成一个完备事件组。
所以根据贝叶斯公式,
\[\mathbb{P}(A_2|B)=\frac{\mathbb{P}(B,A_2)}{\mathbb{P}(B)}=\frac{\mathbb{P}(B|A_2)\mathbb{P}(A_2)}{\sum_i\mathbb{P}(B|A_i)\mathbb{P}(A_i)}=\frac{0.82\times0.5}{0.65\times0.3+0.82\times0.5+0.5\times0.2}=0.58\]
作业题:
假设在考试的多项选择中,考生知道正确答案的概率为 p,猜测答案的概率为 1-p,并且假设考生知道正确答案答对题的概率为1,猜中正确答案的概率为 1/m,其中m为多选项的数目。那么已知考生答对题目,求他知道正确答案的概率。
解:令 B 表示某一考生答对题目这一随机事件,
\(A_1\) 表示知道正确答案的学生,则 \(\mathbb{P}(A_1)=p,\mathbb{P}(B|A_1)=1\)
\(A_2\) 表示猜答案的学生,则 \(\mathbb{P}(A_2)=1-p,\mathbb{P}(B|A_2)=1/m\)
因为 \(\mathbb{P}(A_1)+\mathbb{P}(A_2)=1\) ,所以 \(A_1\) 和 \(A_2\) 组成一个完备事件组。
所以根据贝叶斯公式,
\[\mathbb{P}(A_1|B)=\frac{\mathbb{P}(B,A_1)}{\mathbb{P}(B)}=\frac{\mathbb{P}(B|A_1)\mathbb{P}(A_1)}{\sum_i\mathbb{P}(B|A_i)\mathbb{P}(A_i)}=\frac{1\times p}{1\times p+(1-p)\times 1/m}=\frac{mp}{(m-1)p+1}\]
二、随机变量及其分布:pmf/pdf、CDF、均值、方差¶
Indices and tables¶
Install $project by running:
Euler’s identity, equation (1), was elected one of the most beautiful mathematical formulas.
Since Pythagoras, we know that \(a^2 + b^2 = c^2\).
way2
\[\begin{split}(a + b)^2 &= (a + b)(a + b) \\ &= a^2 + 2ab + b^2\end{split}\]
way3
\[(a + b)^2 = a^2 + 2ab + b^2\]
Look how easy it is to use $a_a$:
- import project
# Get your stuff done project.do_stuff()
Contribute¶
- Issue Tracker: https://github.com/iphysresearch/Math_ML/issues
- Source Code: https://github.com/iphysresearch/Math_ML
Support¶
If you are having issues, please let us know. We have a mailing list located at: hewang@mail.bnu.edu.cn
License¶
The project is licensed under the MIT license.
Footnotes
| [统计独立性] | 当且仅当两个随机事件 A 与 B 满足 \(\mathbb{P}(A\cap B)=\mathbb{P}(A)\mathbb{P}(B)\) 时,事件 A 与 B 才是统计独立的。同样,对于两个独立事件 A 与 B 有 \(\mathbb{P}(A|B)=\mathbb{P}(A)\) 以及 \(\mathbb{P}(B|A)=\mathbb{P}(B)\)。 |
| [互斥性] | 当且仅当两个随机事件 A 与 B 满足 \(\mathbb{P}(A|B)=0\) 且 \(\mathbb{P}(A)\neq0,\mathbb{P}(B)\neq0\) 时,事件 A 与 B 是互斥的。因此,对于两个独立事件 A 与 B 有 \(\mathbb{P}(A|B)=0\) 以及 \(\mathbb{P}(B|A)=0\)。 |